matematicas
martes, 28 de mayo de 2013
domingo, 26 de mayo de 2013
FUNCION LOGARITMO
Una función logarítmica es aquella que genéricamente se expresa como f (x) == logax, siendo a la base de esta función, que ha de ser positiva y distinta de 1.
La función logarítmica es la inversa de la función exponencial (ver t35), dado que:
loga x = b Û ab = x.

Representación gráfica de funciones logarítmicas y de sus inversas (exponenciales).
loga f (x) = loga g (x)
Entonces, se emplean los antilogaritmos para simplificar la ecuación hasta f (x) = g (x), que se resuelve por los métodos habituales.
También puede operarse en la ecuación logarítmica para obtener una ecuación equivalente del tipo:
loga f (x) = m
de donde se obtiene que f (x) = am, que sí se puede resolver de la forma habitual.
 Forma de las funciones logarítmicas según el valor de la base.
Forma de las funciones logarítmicas según el valor de la base.
La función logarítmica es la inversa de la función exponencial (ver t35), dado que:
loga x = b Û ab = x.

Representación gráfica de funciones logarítmicas y de sus inversas (exponenciales).
Propiedades de la función logarítmica
Las propiedades generales de la función logarítmica se deducen a partir de las de su inversa, la función exponencial. Así, se tiene que:- La función logarítmica sólo existe para valores de x positivos, sin incluir el cero. Por tanto, su dominio es el intervalo (0,+¥).
- Las imágenes obtenidas de la aplicación de una función logarítmica corresponden a cualquier elemento del conjunto de los números reales, luego el recorrido de esta función es R.
- En el punto x = 1, la función logarítmica se anula, ya que loga 1 = 0, en cualquier base.
- La función logarítmica de la base es siempre igual a 1.
- Finalmente, la función logarítmica es continua, y es creciente para a > 1 y decreciente para a < 1.
Ecuaciones logarítmicas
Cuando en una ecuación la variable o incógnita aparece como argumento o como base de un logaritmo, se llama logarítmica. La resolución de ecuaciones logarítmicas se basa en los mismos procedimientos utilizados en la resolución de las ecuaciones habituales. Aunque no existen métodos fijos, habitualmente se procura convertir la ecuación logarítmica en otra equivalente donde no aparezca ningún logaritmo. Para ello, se ha de intentar llegar a una situación semejante a la siguiente:loga f (x) = loga g (x)
Entonces, se emplean los antilogaritmos para simplificar la ecuación hasta f (x) = g (x), que se resuelve por los métodos habituales.
También puede operarse en la ecuación logarítmica para obtener una ecuación equivalente del tipo:
loga f (x) = m
de donde se obtiene que f (x) = am, que sí se puede resolver de la forma habitual.
Sistemas de ecuaciones logarítmicas
Cuando en un sistema aparecen una o varias ecuaciones logarítmicas, se denomina sistema de ecuaciones logarítmicas. En el caso de un sistema de dos ecuaciones con dos incógnitas, se pueden producir tres casos distintos:- Un sistema formado por una ecuación polinómica y una logarítmica.
- Un sistema constituido por dos ecuaciones logarítmicas.
- Un sistema compuesto por una ecuación polinómica y una ecuación exponencial.
 Forma de las funciones logarítmicas según el valor de la base.
Forma de las funciones logarítmicas según el valor de la base.sábado, 25 de mayo de 2013
FUNCION EXPONENCIAL
La función exponencial es del tipo:
Sea a un número real positivo. La función que a cada número real x le hace corresponder la potencia ax se llama función exponencial de base a y exponente x.
| x | y = 2x |
|---|---|
| -3 | 1/8 |
| -2 | 1/4 |
| -1 | 1/2 |
| 0 | 1 |
| 1 | 2 |
| 2 | 4 |
| 3 | 8 |


| x | y = 2x |
|---|---|
| -3 | 8 |
| -2 | 4 |
| -1 | 2 |
| 0 | 1 |
| 1 | 1/2 |
| 2 | 1/4 |
| 3 | 1/8 |

Propiedades de la función exponencial
Dominio:  .
.
 .
.
Recorrido:  .
.
Es continua.
Los puntos (0, 1) y (1, a) pertenecen a la gráfica.
Es inyectiva  a ≠ 1(ninguna imagen tiene más de un original).
a ≠ 1(ninguna imagen tiene más de un original).
Creciente si a >1.
Decreciente si a < 1.
Las curvas y = ax e y = (1/a)x son simétricas respecto del eje OY.

- La función exponencial existe siempre para cualquier valor de la variable independiente x.
- Toma valores positivos para cualquier valor de x.
- El dominio de la función exponencial es todo el conjunto de los números reales.
- Todas las funciones pasan por el punto (0,1).
- Las gráficas de las funciones exponenciales de la forma f(x)=bx, con b>1 son crecientes. Los valores de la función crecen cuando x aumenta.
- Las gráficas de las funciones exponenciales de la forma f(x)=bx, con 0<b<1 son decrecientes. Los valores de la función decrecen cuando x aumenta.
- El eje x es una asíntota horizontal, hacía la izquierda si b>1 y hacía la derecha si b<1.
- La definición exige que la base sea positiva y diferente de uno.
- Si b=0 la función se transforma en la función constante 0.
Para resolver estas ecuaciones se suelen utilizar dos métodos alternativos:
- Igualación de la base: consiste en aplicar las propiedades de las potencias para lograr que en los dos miembros de la ecuación aparezca una misma base elevada a distintos exponentes: Ax = Ay.
En tales condiciones, la resolución de la ecuación proseguiría a partir de la igualdad x = y. - Cambio de variable: consiste en sustituir todas las potencias que figuran en la ecuación por potencias de una nueva variable, convirtiendo la ecuación original en otra más fácil de resolver. 22x - 3 × 2x - 4 = 0
t2 - 3t - 4 = 0
FUNCION RACIONAL
Las funciones racionales son funciones obtenidas al dividir un polinomio por otro polinomio distinto de cero. Para una única variable x una función racional se puede escribir como:
P (x)
f(x) = -------
Q (x)
donde P y Q son polinomios y x es una variable indeterminada siendo Q un polinomio no nulo. Existe la posibilidad de encontrar valores de x tales que Q(x) sea igual a cero. Por este motivo las funciones racionales están definidas en todos los números que no anulan el polinomio denominador, es decir, en el cuerpo de coeficientes menos una cantidad finita, que será igual al número de raíces reales del polinomio denominador. Una función racional está definida en todo el cuerpo de coeficientes si el polinomio denominador no tiene raíces reales.
El dominio lo forman todos los números reales excepto los valores de x que anulan el denominador.
ASINTOTA VERTICAL
Las asíntotas verticales son rectas verticales a las cuales la función se va acercando indefinidamente sin llegar nunca a cortarlas
OJO: No debe confundirse la condición de que una asíntota vertical no se toca o cruza, con el hecho, de que las funciones sí pueden cruzar o tocar una asíntota horizontal, pero eso lo explicare mas tarde.
Para que una función tenga una o varias asíntotas verticales, se tienen que cumplir las siguientes condiciones:
1.- En x = a, la función no está definida, o sea, x = a no es parte del dominio de la función. Por esto no la puede tocar.
2.- El límite cuando x tiende a "a" de la función no existe, pero tiene que haber una tendencia de la función hacia valores extremadamente grandes (infinito) ó extremadamente negativos (menos infinito). Puede darse el caso, de que acercándose por ambos lados al valor de x = a, la tendencia del valor de la función sean ambos infinitos ó ambos menos infinito.
ASINTOTA HORIZONTAL
Las asíntotas horizontales se refieren a la tendencia de una función. Las tendencias se descubren calculando los límites de la función para valores muy grandes (infinitos) o para valores muy negativos (menos infinito).
Las asíntotas horizontales pueden ser bilaterales en un mismo valor, bilaterales con diferente valor, o unilaterales.
Hay funciones en las cuales las asíntotas horizontales no se tocan ni cruzan, hay otras en las cuales sí se puede cruzar la asíntota horizontal.No hay que confundir, que las asíntotas verticales no se pueden tocar ni cruzar, ya que ellas dependen de las no definiciones de la función, y si la función no está definida en una asíntota vertical, no puede adoptar el valor de x de la asíntota vertical.
Aquí se van a analizar funciones que presentan asíntotas horizontales:
1.- Desde el punto de vista funciones racionales sólo hay dos tipos que presentan asíntotas horizontales; las que tienen el grado del numerador igual o menor que el grado del denominador.
2.- También presentan asíntotas horizontales algunas funciones exponenciales así como algunas logarítmicas.
¿Como se determinan las asintota?
->Las asíntotas verticales se determinan de la siguiente manera:
Se determinan encontrando las raíces del denominador h(x) correspondiente. tales valores reciben el nombre de polos en la función. Entonces el numero de polo asociados en una función determinaran el numero de asíntotas verticales que tiene tal función.ejemplo:
f(x):=4x-4
Sabemos que en los casos en los cuales h(x)=0 , la función se indetermina es decir su valor se tiende a infinito.
x-4=0 ; es decir en: x=4
La recta x=4 es la asíntota de esta función, que es única , ya que el denominador es un termino lineal lo que implica que solamente en un valor se anula. En la siguiente gráfica correspondiente veremos que a medida en que x se aproxima a 4 el cociente aumenta indefinidamente.
->Las asintotas horizontales se determinan de la siguiente manera:
Se encuentran presentes únicamente en funciones racionales de la forma
f(x)=g(x)/h(x)
Y se determinan haciendo que la variable independiente “x” tienda al infinito lo que trae como consecuencia que la función cociente tienda a un valor determinado fijo , al que nunca va a llegar, ni mucho menos sobrepasar. Es decir que es la recta dada por el cociente de los coeficientes de grado mayor.
ejemplo:
f(x):=(4x+1)x-2
La asíntota vertical se encuentra en el polo de la función que en esta caso esta en:
X-2=0
X=2
Es decir, la recta x=2 es la asíntota vertical.
f(x):=(4x+1)x-2
La asíntota horizontal se encuentra en el cociente de los términos de mayor exponente como ya se indico. La recta y=4 es la asíntota horizontal como se muestra en la figura anterior.
¿Que es una discontinuidad?
Una discontinuidad es un punto de una función y=f(x) en la cual la misma sufre un "salto" o cambio "brusco" de valor. Se verifica una discontinuidad cuando el valor de la función en un punto difiere del límite de esa función cuando nos acercamos a ese punto por derecha y por izquierda.
Si alguna de las tres condiciones de continuidad no se cumple, la función es discontinua:
La función es discontinua porque no existe imagen
La función es discontinua porque no tiene límite.
La función es discontinua porque no coincide la imagen con el límite.
Ejemplos
a)- En este ejemplo tenemos la siguiente función.
f(X)=x+1/x-1
- Para poder determinar la asíntota vertical usamos el polinomio que esta como denominador, y lo igualamos a 0 y despejamos.
X-1=0 x=1
-Para obtener la asintonta horizontal usamos el grado superior de dominador y del numerador que en este caso los dos tienes x, así que agarramos los coeficientes del numerador y denominador.
f(x)=y=1/1
y=1
x
|
y
|
-3.7
|
0.5744
|
-2.4
|
0.4117
|
-1.1
|
0.0476
|
0.2
|
-1.5
|
1.5
|
5
|
2.8
|
2.111
|
4.1
|
1.6451
|
b)
f(x)=2/x+3
- Para poder determinar la asíntota vertical usamos el polinomio que esta como denominador, y lo igualamos a 0 y despejamos.
4+x=0 -3=x
x
|
y
|
-7
|
0.5
|
-4.4
|
1.428
|
-3.1
|
-20
|
-1.8
|
-1.666
|
0.5
|
0.8
|
2.1
|
0.3921
|
4.7
|
0.2597
|
DIVISION SINTETICA
La división sintética se realiza para simplificar la división de un polinomio entre otro polinomio de la forma x – c, logrando una manera mas compacta y sencilla de realizar la división.
Ilustraremos como el proceso de creación de la división sintética con un ejemplo:
Comenzamos dividiéndolo normalmente
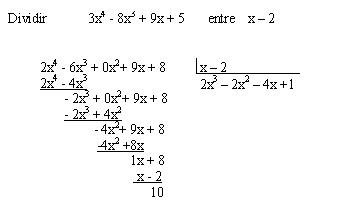 Pero resulta mucho escribir pues repetimos muchos términos durante el procedimiento, los términos restados
Pero resulta mucho escribir pues repetimos muchos términos durante el procedimiento, los términos restados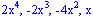 pueden quitarse sin crear ninguna confusión, al igual que no es necesario bajar los términos
pueden quitarse sin crear ninguna confusión, al igual que no es necesario bajar los términos 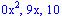 . al eliminar estos términos repetidos el ejercicio nos queda:
. al eliminar estos términos repetidos el ejercicio nos queda:
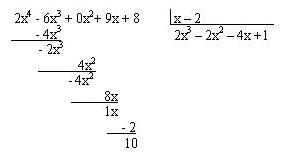 Ahora si mantenemos las potencias iguales de x en las columnas de cada potencia y colocando 0 en las faltantes se puede eliminar el escribir las potencias de x, así:
Ahora si mantenemos las potencias iguales de x en las columnas de cada potencia y colocando 0 en las faltantes se puede eliminar el escribir las potencias de x, así:
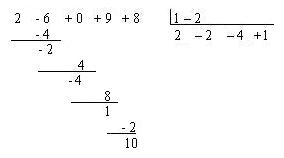 Como para este tipo de división solo se realiza con para divisores de la forma x – c entonces los coeficientes de la parte derecha siempre son 1 – c, por lo que podemos descartar el coeficiente 1 y el signo negativo, también se puede lograr una forma más compacta al mover los números hacia arriba, nos queda de la siguiente forma:
Como para este tipo de división solo se realiza con para divisores de la forma x – c entonces los coeficientes de la parte derecha siempre son 1 – c, por lo que podemos descartar el coeficiente 1 y el signo negativo, también se puede lograr una forma más compacta al mover los números hacia arriba, nos queda de la siguiente forma:
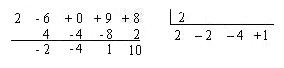 Si ahora insertamos a la primera posición del último renglón al primer coeficiente del residuo (2), tenemos que los primeros números de este renglón son los mismos coeficientes del cociente y el último número es el residuo, como evitamos escribir dos veces eliminamos el cociente.
Si ahora insertamos a la primera posición del último renglón al primer coeficiente del residuo (2), tenemos que los primeros números de este renglón son los mismos coeficientes del cociente y el último número es el residuo, como evitamos escribir dos veces eliminamos el cociente.
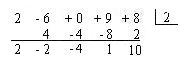 Esta última forma se llama división sintética, pero ¿como hacerla sin tanto paso?, ahora les presentamos los pasos para llevar a cavo la división sintética:
Esta última forma se llama división sintética, pero ¿como hacerla sin tanto paso?, ahora les presentamos los pasos para llevar a cavo la división sintética:
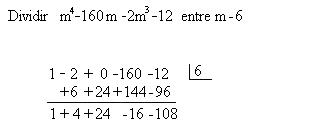
 Donde 748 es el residuo y pese a no tener muchos coheficientes vemos que en el resultado si aparecen todos los coheficientes nesesarios para todos los exponentes.
Donde 748 es el residuo y pese a no tener muchos coheficientes vemos que en el resultado si aparecen todos los coheficientes nesesarios para todos los exponentes.
Para generalizar hace falta notar que el signo que tenga el divisor no debe ser necesariamente negativo. Para el uso de este método puede ser positivo o negativo.
Ejemplo:
Sean y
y  polinomios tales que:
polinomios tales que: 
Determine el cociente y el residuo que se obtiene al dividir por
por  : a) Usando el método (División larga) b) Usando división sintética
: a) Usando el método (División larga) b) Usando división sintética
Solución:
a)

b) Usando división sintética, se divide por
se divide por  de la siguiente manera:
de la siguiente manera:
 Donde los números 4, 15 y 40 son los coeficientes del cociente y 122 el residuo de la división. Observe que, según la parte (a) de este ejercicio, los números obtenidos en la tercera fila son los coeficientes del cociente y el residuo, como se muestra en el esquema anterior. Los números representados en la primera fila son los coeficientes de
Donde los números 4, 15 y 40 son los coeficientes del cociente y 122 el residuo de la división. Observe que, según la parte (a) de este ejercicio, los números obtenidos en la tercera fila son los coeficientes del cociente y el residuo, como se muestra en el esquema anterior. Los números representados en la primera fila son los coeficientes de  (dividendo) y el cero de
(dividendo) y el cero de  (divisor). Los números representados en la segunda fila se obtienen de la siguiente forma:
(divisor). Los números representados en la segunda fila se obtienen de la siguiente forma:
12 es el producto de 4 y 3
45 es el producto de 15 y 3
120 es el producto de 40 y 3 Los números representados en la tercera fila se obtienen de la siguiente forma:
4 es el coeficiente de en
en 
15 es la suma de 3 y 12
40 es la suma de -5 y 45
122 es la suma de 2 y 120 Ejemplo: Sean y
y  polinomios tales que:
polinomios tales que:  .
.
Usando división sintética, determine el cociente y el residuo
y el residuo  que se obtiene al dividir
que se obtiene al dividir  por
por  . Solución:
. Solución:
Ordenando en forma desendiente de acuerdo a su grado, se obtiene:
en forma desendiente de acuerdo a su grado, se obtiene:
 , y realizando la división se tiene:
, y realizando la división se tiene:

Por lo que  o sea
o sea  y
y  Nota: Observe que al realizar la división sintética, tanto los coeficientes del dividendo que son diferentes de cero, como los que son iguales a cero, debem escribirse. Ejemplo: Sean
Nota: Observe que al realizar la división sintética, tanto los coeficientes del dividendo que son diferentes de cero, como los que son iguales a cero, debem escribirse. Ejemplo: Sean  y
y  polinomios tales que:
polinomios tales que:  y
y 
Usando división sintética determine el cociente y
y  . Solución: Como
. Solución: Como  y el cero
y el cero  es -4 tenemos que:
es -4 tenemos que:
 Por lo tanto el cociente que se obtiene, al dividir
Por lo tanto el cociente que se obtiene, al dividir  por
por  es
es  y el residuo es -68. Ejercicio:
y el residuo es -68. Ejercicio:
Para cada par de polinomios y
y  que se definen acontinuación determine por división sintética el cociente y el residuo que se obtiene al dividir
que se definen acontinuación determine por división sintética el cociente y el residuo que se obtiene al dividir  por
por  .
.
Ejemplo: Sea  un polinomio tal que:
un polinomio tal que:  ; usando división sintética determine
; usando división sintética determine  y
y 
Solución:
Recuerde que es igual al residuo que se obtiene al dividir
es igual al residuo que se obtiene al dividir  por
por  .
.
Efectuando las divisiones correspondientes se tiene:
 Ejercicio:
Ejercicio:
Sea un polinomio tal que
un polinomio tal que  Usando división sintética determine
Usando división sintética determine  .
.
Ilustraremos como el proceso de creación de la división sintética con un ejemplo:
Comenzamos dividiéndolo normalmente
- Se ordenan los coeficientes de los términos en un orden decreciente de potencias de x hasta llegar al exponente cero rellenando con coeficientes cero donde haga falta
- Después escribimos “c” en la parte derecha del renglón
- Se baja el coeficiente de la izquierda al tercer renglón.
- Multiplicamos este coeficiente por “c” para obtener el primer numero del segundo renglón (en el primer espacio de la izquierda nunca se escribe nada).
- Simplificamos de manera vertical para obtener el segundo número de el tercer renglón.
- Con este último número repetimos los pasos cuatro y cinco hasta encontrar el último número del tercer renglón, que será el residuo.
Donde -108 es el residuo
Para generalizar hace falta notar que el signo que tenga el divisor no debe ser necesariamente negativo. Para el uso de este método puede ser positivo o negativo.
Sean
Determine el cociente y el residuo que se obtiene al dividir
Solución:
a)

| Por lo que al dividir |
b) Usando división sintética,
 Donde los números 4, 15 y 40 son los coeficientes del cociente y 122 el residuo de la división. Observe que, según la parte (a) de este ejercicio, los números obtenidos en la tercera fila son los coeficientes del cociente y el residuo, como se muestra en el esquema anterior. Los números representados en la primera fila son los coeficientes de
Donde los números 4, 15 y 40 son los coeficientes del cociente y 122 el residuo de la división. Observe que, según la parte (a) de este ejercicio, los números obtenidos en la tercera fila son los coeficientes del cociente y el residuo, como se muestra en el esquema anterior. Los números representados en la primera fila son los coeficientes de 12 es el producto de 4 y 3
45 es el producto de 15 y 3
120 es el producto de 40 y 3 Los números representados en la tercera fila se obtienen de la siguiente forma:
4 es el coeficiente de
15 es la suma de 3 y 12
40 es la suma de -5 y 45
122 es la suma de 2 y 120 Ejemplo: Sean
Usando división sintética, determine el cociente
Ordenando

| Los números 1, 0, 0 y 2 son coeficientes del cociente. Y el número 0 es el residuo. |
Usando división sintética determine el cociente
 Por lo tanto el cociente que se obtiene, al dividir
Por lo tanto el cociente que se obtiene, al dividir Para cada par de polinomios
| 1. | |
| 2. | |
| 3. | |
| 4. | |
| 5. | |
| 6. |
Solución:
Recuerde que
Efectuando las divisiones correspondientes se tiene:
 Ejercicio:
Ejercicio: Sea
Suscribirse a:
Entradas (Atom)